формули комбінаторної геометрії

    Задачі розфарбування з використанням методу Діріхле.

                                

                                                       А

 Задача 1. У кожній вершині правильного 100-кутника розташовані фішки: 76 червоних та 24 синіх. Довести, що знайдуться 4 червоні фішки, що утворюють квадрат.

Розв’язання: Зрозуміло, що 100 фішок можуть утворити 100:4=25 квадратів, тому (по одній синій фішці у кожного квадрата) сині вершини будуть мати не більше 24 квадратів, отже, один квадрат

буде мати червоні вершини.

Задача 2. У кожній вершині правильного 2005-кутника розташовані фішки:1605 червоних та 400 синіх. Довести, що знайдуться 5 червоні фішки, що утворюють правильний п’ятикутник.

Розв’язання: В правильному 2005-кутнику можна утворювати правильні п’ятикутники так: між будь-якими двома вершинами п’ятикутника повинна знаходиться рівно 400 вершин даної фігури.  Зрозуміло, що 2005 фішок можуть утворити 2005:5=401 правильних п’ятикутників, тому (по одній синій фішці у кожного правильного п’ятикутника) сині вершини будуть мати не більше 400 п’ятикутника, отже, один п’ятикутник буде мати червоні вершини.

Задача 3. У кожній вершині правильного 2004-кутника розташовані фішки:1838 червоних та 166 синіх. Довести, що знайдуться 12 червоних  фішки, що утворюють правильний 12-кутник.

Розв’язання: В правильному 2004-кутнику можна утворювати правильні 12-кутники так: між будь-якими двома вершинами 12-кутника повинна знаходиться рівно 166 вершин даної фігури.  Зрозуміло, що 2004 фішки можуть утворити 2004:12=167 правильних 12-кутників, тому (по одній синій фішці у кожного правильного 12-кутника) сині вершини будуть мати не більше 400 п’ятикутника, отже, один п’ятикутник буде мати червоні вершини.

Задача 4. У кожній вершині правильного 24-кутника розташовані фішки:21 червоних та 3 синіх. Довести, що знайдуться 6 червоних  фішки, що утворюють правильний 6-кутник.

Розв’язання: В правильному 24-кутнику можна утворювати правильні 6-кутники так: між будь-якими двома вершинами 6-кутника повинна знаходиться рівно 3 вершини даної фігури.  Зрозуміло, що 2004 фішки можуть утворити 24:6=4 правильних 6-кутників, тому (по одній синій фішці у кожного правильного 6-кутника) сині вершини будуть мати не більше три 6-кутника, отже. один 6-кутник буде мати червоні вершини.

                          

                                             Б

Задача 5. Площина пофарбована у два кольори. Довести, що знайдуться 2 точки на відстані 1 м  : а) одного кольору; б) різних кольорів.

Розв’язання: а)Якщо на зафарбованій у два кольори площині побудувати правильний трикутник зі стороною 1м, то із трьох його вершин у крайньому разі дві будуть одного кольору. За принципом Діріхле, адже вершин 3, а кольорів всього 2. Вершини одного кольору і утворюють шукані точки.

Б) На відстані не менше одного метра візьмемо дві точки А та В. Нехай ці точки різного кольору. Їх завжди можна вибрати різного кольору. Побудуємо рівнобедрений трикутник АВС, АС=СВ=1 м. Колір точки С відмінний від кольору однієї із точок А,В.

Задача 6. Площина пофарбована у три кольори. Довести, що знайдуться 2 точки на відстані  1 м  одного кольору.

Розв’язання: Доведемо, способом від супротивного. Допустимо, що будь-які дві точки, що лежать на даній площині на відстані 1м різного кольору. Розглянемо правильний трикутник АВС зі стороною 1 м. Усі його вершини різного кольору. Нехай точка А₁ симетрична А відносно прямої ВС. За припущенням вершини рівностороннього трикутника   А₁ ВС різного кольору. А₁В=А₁С. Але точки А та А₁ одного кольору.

Ці міркування  показують, що якщо АА₁=√3 , то точки А та А₁ одного кольору. Тому всі точки кола радіуса √3 з центром А одного кольору. Зрозуміло, що на цій точці знайдуться дві точки одного кольору. Це протиріччя доводить існування двох точок , відстань між якими 1м.

      

       Задачі на  розфарбування у шаховому порядку

   

                                         А

Задача 7. Чи можна викласти квадрат  розміром 6х6 клітинок

 фігурками виду Т, які містять тільки чотири клітинки?

Розв’язання: Доведемо , що не можна. Скористаємося методом від

 супротивного. Допустимо, що можна викласти даними фігурками

квадрат. Розфарбуємо всі клітини квадрата 6х6 у шаховому порядку.

 Кожна фігурка виду Т містить або 1, або 3 однокольорові клітинки.

Для визначеності візьмемо чорні клітинки. У 9 фігурках їх непарна

 кількість. Отже, маємо протиріччя з тим, що загальна кількість

  чорних клітинок квадрату 6х6 рівна 18.

Відповідь: не можна.

Задача 8. На трикутній політичній карті розміром 7 м, 7м, 7м є 49

 однакових за площею трикутних держав. За домовленістю

будь-яка держава континенту кожного року направляє делегацію

 тільки в одну з держав, з якою має суцільну ділянку кордону.

 Чи усі держави такої політичної карти приймають делегацію

 кожного року?

Розв’язання: Розфарбуємо 49 рівносторонніх трикутників політичної

 карти у два, білий та чорний кольори так, щоб по обидві сторони

 будь-якого трикутника лежали різні кольори. Нехай чорних кольорів

 більше, якщо це не так, то перефарбуємо у протилежні кольори.

 Отже, чорних держав більше, ніж білих. Так, як кожна держава

 надсилає делегацію у протилежну за кольором державу, то  хоча б

 одній чорній державі не  вистачить  делегації з білої держави.   

Відповідь : не всі.

                Задачі на розрізання геометричних фігур.

Задача  9. Минулого року на ромбічній політичній карті зі сторонами

 3 м та гострими кутами 60⁰ було 18 однакових за площею та трикутних

  за формою держав, у яких усі ділянки кордонів рівні 1 м. Цього

 року держави утворили дві однакові за площею та шестикутні

 за формою федерації та декілька ромбічних за формою федерацій.

 Будь-які дві держави  федерації  мають суцільну ділянку кордону.

Чи усі держави минулорічної політичної карти увійшли до федерацій?

 Яку найбільшу кількість  ромбічних та шестикутних федерацій можна

 утворити на минулорічній політичній карті?

Розв’язання: Дві шестикутні федерації знаходяться по обидві сторони

 від меншої діагоналі , кожна з яких складається з шести трикутних

 держав. Дві трикутні держави , що знаходяться у вершинах гострих

кутів минулорічної  політичної карти не можуть увійти до будь-якої

федерації, бо у противному випадку на політичній карті не можна

розмістити дві шестикутні федерації. Отже, можна розмістити на

 політичній карті чотири федерації, з яких дві ромбічні.

Відповідь : не всі, 4.

Задача  10. Чи можна стоклітинкову  квадратну дошку розрізати

на плитки розміром 1х4?

Розв’язання: Розфарбуємо дану дошку у чотири кольори

діагональним чином. Різна кількість другого та четвертого

кольорів, а кожна плитка мала б містити усі чотири кольори.

Відповідь: не можна.

Задача  11. Чи можна  будь-який  чотирикутник  розфарбувати на

 вісім кольорів так, щоб кожен колір обмежувався рівнобедреним

трикутником, а  потім будь-який  з цих кольорів перефарбувати

 на три чотирикутники?

Розв’язання: Розділимо  довільний чотирикутник  діагоналлю,

 що з’єднує найбільші  протилежні кути. Утвориться два довільні

трикутники. У  цих двох трикутниках проведемо висоти до найдовших

сторін. Отримаємо чотири прямокутних трикутника, на які розрізано

  даний чотирикутник. У кожному прямокутному трикутнику 

проведемо медіану до найдовшої сторони. Отримаємо  необхідних

 нам вісім рівнобедрених трикутників. Ці трикутники  рівнобедрені

 так, як медіана , що проведена до гіпотенузи, рівна половині

гіпотенузи прямокутного трикутника. Розфарбуємо даний

 чотирикутник у  вісім кольорів. В середині кожного пофарбованого

 трикутника  візьмемо точку та  проведемо від неї до кожної

 сторони трикутника перпендикуляри. Утворимо розбиття

 пофарбованого трикутника  на три чотирикутника.

Їх і необхідно перефарбувати.

Відповідь: можна

Задача  12. Як будь-який  трикутник  розфарбувати на найменшу

кількість чотирикутників , у яких діагоналі перпендикулярні?.

Розв’язання: В середині трикутника візьмемо точку перетину

 бісектрис  та  проведемо від неї до кожної сторони трикутника

перпендикуляри. Ці перпендикуляри рівні радіусу вписаного

 в трикутник кола.  Утворимо розбиття пофарбованого трикутника

на три чотирикутника, тобто дельтоїда, у яких перпендикулярні

 діагоналі. Менше чотирикутників  утворити не можна. Їх і необхідно перефарбувати.

Задача  13. Як будь-який  трикутник  розфарбувати на  чотири

 рівних між собою трикутників?.

Розв’язання: В трикутнику три середні лінії. Отримаємо потрібне

 розфарбування.

Задача  14. Як будь-який рівнобедрений трикутник  розфарбувати

 на  найменшу кількість рівновеликих  між собою чотирикутників?

Розв’язання: В трикутнику з’єднати точку перетину медіан та

 середини сторін. Отримаємо потрібне розфарбування.

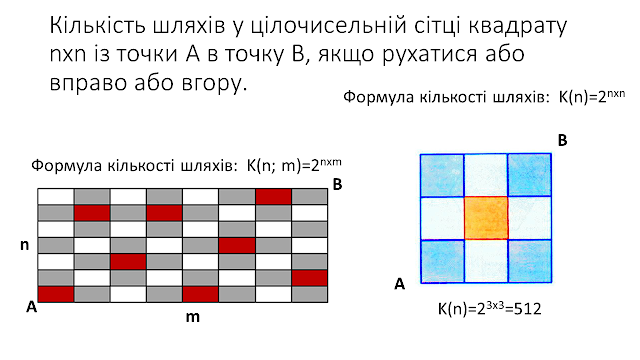
11.Створити в MS Excel на Аркуш 11  формулу(функцію), що за кількістю  непаралельних прямих на площині    знаходить кількість  утворених частин площини, при умові, що кожна точка перетину прямих утворена не більше, ніж двома прямими. Протабулювати цю функцію для  n ={4;5;6;7;8;9;10;11;12;13;14}.  Створити за даними таблиці лінійну діаграму з назвою: «Кількість частин площини, що утворена прямими».

Розв’язання. Якщо зафіксуємо деяку чотири частини для двох прямих, тоді  тільки  третя  пряма додає ще три частини площини, і так далі.  Таких  частин можна порахувати, використовуючи комбінації 1+ С _n+1², якщо кожна точка утворена  тільки однією парою прямих.  Формула кількості точок перетину n непаралельних прямих має вигляд:  k(n)=  (n+1)n/2 +1, де n - натуральне число.

.  Формула кількості точок перетину n непаралельних прямих має вигляд:  k(n)= (n+1)n/2 +1, де n - натуральне число.

12.Створити в MS Excel на Аркуш 12  формулу(функцію), що за кількістю  непаралельних площин  у простoрі   знаходить кількість  утворених частин простору, при умові, що кожна пряма  перетину площин  утворена не більше, ніж двома площинами. Протабулювати цю функцію для  n ={4;5;6;7;8;9;10;11;12;13;14}.  Створити за даними таблиці лінійну діаграму з назвою: «Кількість частин простору, що утворена площинами».

Розв’язання.  Формула кількості частин  n непаралельних площинами загального положення має вигляд:  k(n)=  (n+1)(n²-n+6)/6, де n - натуральне число.

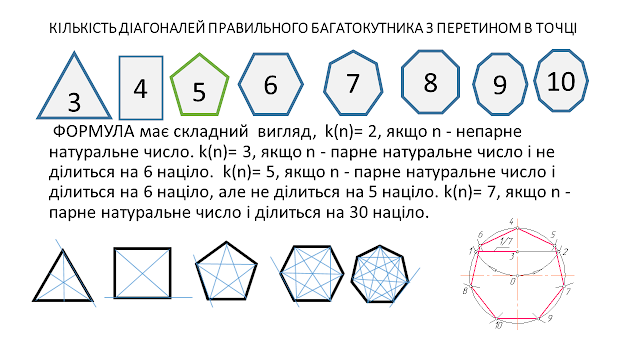
13.Створити в MS Excel на Аркуш 13  формулу(функцію), що за кількістю сторін  правильного n-кутника на площині  знаходить кількість  осьових симетрій фігури у просторі. Протабулювати цю функцію для  n ={4;5;6;7;8;9;10;11;12;13;14}.  Створити за даними таблиці лінійну діаграму з назвою: «Кількість осьових симетрій у просторі для правильного n-кутника на площині».

Розв’язання.  Формула кількості осей симетрій  у просторі правильного n-кутника на площині має вигляд:  k(n)=n+1, де n - натуральне число, більше 2.

14.Створити в MS Excel на Аркуш 14  формулу(функцію), що за заданими n точками  на площині, знаходить кількість  відрізків між ними. Протабулювати цю функцію для  n ={4;5;6;7;8;9;10;11;12;…;24}.  Створити за даними таблиці лінійну діаграму з назвою: «Кількість відрізків на площині».

Розв’язання.  Формула кількості відрізків  за заданими n точками  на площині,  знаходить кількість  відрізків між ними має вигляд:  k(n)=  (n-1)n/2 , де n - натуральне число.

15.Створити в MS Excel на Аркуш 15  формулу(функцію), що за заданими n точками  на площині, знаходить кількість трикутників  утвореними цими точками-вершинами трикутників. Протабулювати цю функцію для  n ={4;5;6;7;8;9;10;11;12;…;18}.  Створити за даними таблиці лінійну діаграму з назвою: «Кількість трикутників на площині».

Розв’язання.  Формула кількості відрізків  за заданими n точками  на площині,  знаходить кількість  відрізків між ними має вигляд:  k(n)=  (n-2)(n-1)n/6 , де n - натуральне число, не менше 3.

16.Створити в MS Excel на Аркуш 16  формулу(функцію), що за заданими n точками  на площині, знаходить кількість будь-яких чотирикутників  утвореними цими точками-вершинами чотирикутників. Протабулювати цю функцію для  n ={4;5;6;7;8;9;10;11;12;…;18}.  Створити за даними таблиці лінійну діаграму з назвою: «Кількість будь-яких чотирикутників на площині».

Розв’язання.  Формула кількості відрізків  за заданими n точками  на площині,  знаходить кількість  відрізків між ними має вигляд:  k(n)=  (n-3)(n-2 )(n-1)n/24 , де n - натуральне число, не менше 3.

17. Створити в MS Excel на Аркуш 17  формулу(функцію), що за заданими n –вершинами  випуклого багатокутника на площині,  які утворені перетином не більше двох діагоналей, знаходить кількість будь-яких внутрішніх частин  утвореними діагоналями і сторонами багатокутника. Протабулювати цю функцію для  n ={4;5;6;7;8;9;10;11;12;…;18}.  Створити за даними таблиці лінійну діаграму з назвою: «Кількість будь-яких чотирикутників на площині».

Розв’язання.  Формула кількості будь-яких внутрішніх частин  утвореними діагоналями і сторонами випуклого багатокутника за заданими n вершинами цього багатокутника на площині має вигляд:  k(n)= (n-2)( (n-1 )(n²-3 n +12)/24 , де n - натуральне число, не менше 3.

18. Створити в MS Excel на Аркуш 18  формулу(функцію), що за заданими n – точками на площині знаходить кількість будь-яких  k-ланкових ламаних (2<k<=n) утвореними цими точками, як вершинами ламаних. Протабулювати цю функцію для  n ={4;5;6;7;8;9;10;11;12;…;18}.  Створити за даними таблиці лінійну діаграму з назвою: «Кількість ламаних на площині».

Розв’язання.  Формула кількості будь-яких  k-ланкових випуклого багатокутника за заданими n вершинами  площині має вигляд:  k(n)= 2ⁿ , де n - натуральне число, не менше 3.

19. Створити в MS Excel на Аркуш 19  формулу(функцію), що за заданими n  нефарбованими  неспівпадаючими точками на площині і k фарбами,  знаходить кількість способів   розфарбувань усіх цих точок.  Протабулювати цю функцію для  n ={4;5;6;7;8;9;10;11;12;…;18},  якщо k =4. Створити за даними таблиці лінійну діаграму з назвою: «Кількість чотирикольорових розфарбувань точок  на площині».

Розв’язання.  Формула кількості способів  розфарбувань  k  ф арбами  заданих  n точками на  площині має вигляд:  m(n; k)= kⁿ , де n, k - натуральне число.

20. Створити в MS Excel на Аркуш 20  формулу(функцію), що за заданими n  триколірних світлофорів у неспівпадаючих  точках  на площині,  знаходить кількість способів   включень в усіх цих точках світлофорів, враховуючи, що світлофори ніколи не вимикаються .  Протабулювати цю функцію для  n ={4;5;6;7;8;9;10;11;12;…;18}.  Створити за даними таблиці лінійну діаграму з назвою: «Кількість способів вмикання світлофорів».

Розв’язання.  Формула кількості способів  розфарбувань  трьома  фарбами  заданих  n точок  на  площині має вигляд:  m(n)= 3ⁿ , де n - натуральне число.